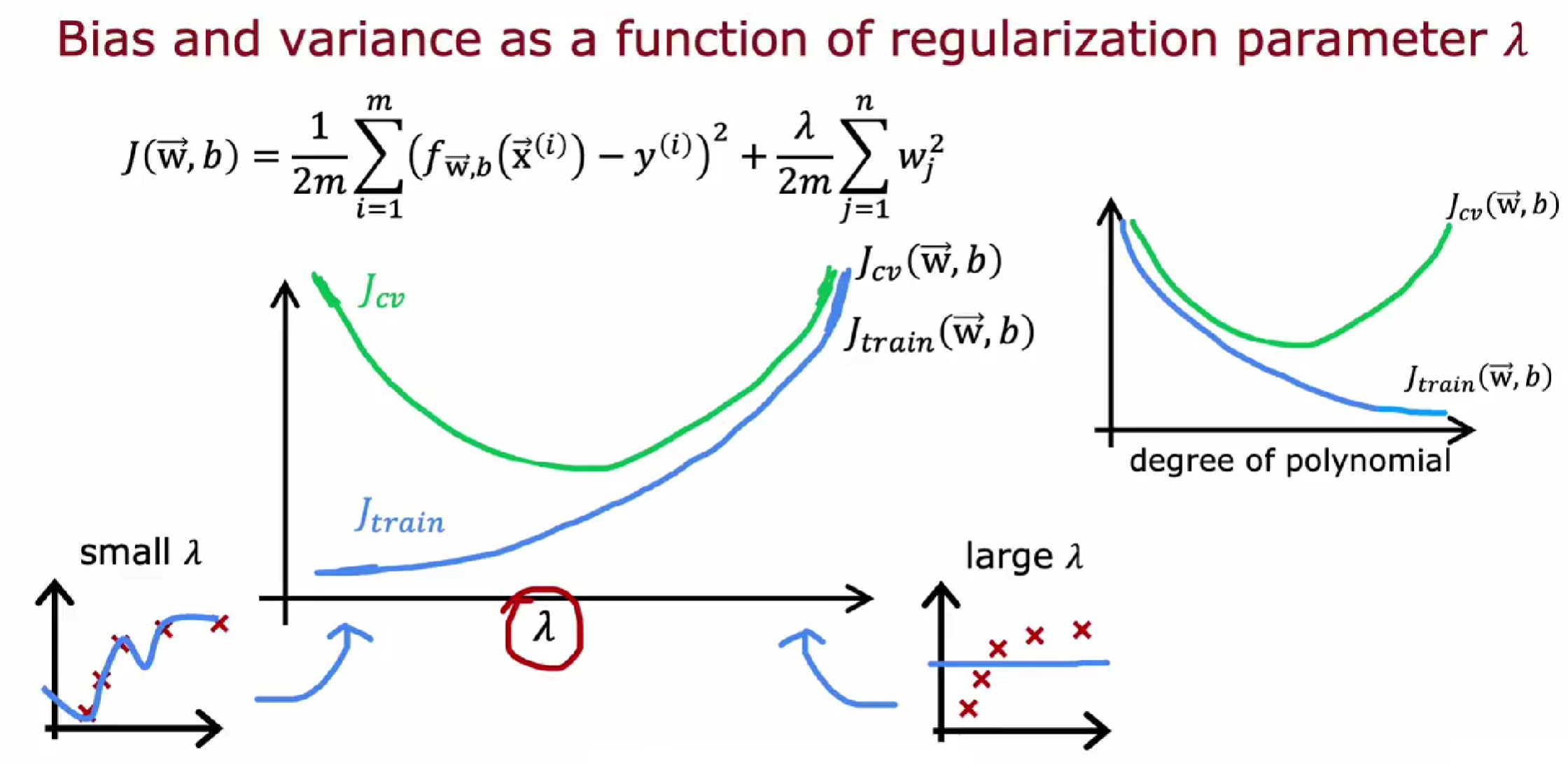
正则化

正则化的使用方法

将正则化应用在代价函数中，使用正则化来减小参数的大小
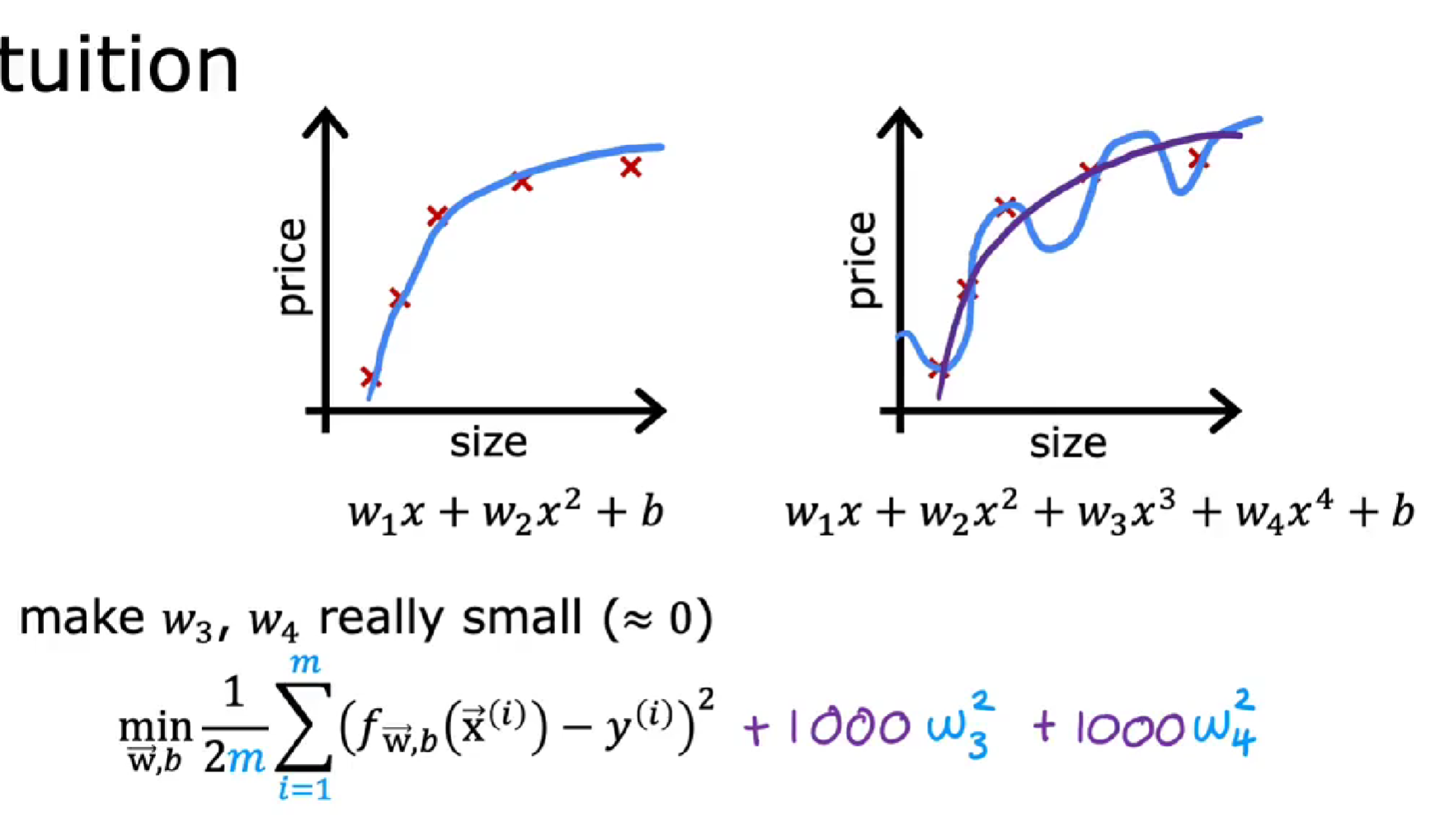
如何理解上式？
因为 $w_3^2$ 和 $w_4^2$ 前的系数非常大，要想使整个式子最小化，只能令 $w_3^2$ 和 $w_4^2$ 非常小（$\approx 0$），$w_3$ 和 $w_4$ 即为惩罚项。
对于右图过拟合状态，此时 $w_3$ 和 $w_4$ 权重衰减，这样就会降低高阶项对整个函数的影响，使得拟合的函数变得比较平滑。
如果有很多的特征，那如何选择惩罚项呢？
如果有非常多的特征，你可能不知道那些特征重要，以及需要惩罚的特征。通常实现正则化的方式是惩罚所有的特征。
对于预测房价实例，比如有 100 个特征，正则化后的代价函数如下：

把上式分为两部分，左边部分即为原始的代价函数，右边部分为正则化项。λ为超参数，通常会取一个较大的数。
为了最小化整个代价函数，当λ是固定的，那么就要减小 $w_1$ 到 $w_n$ 的值。加入正则项后，$w_1$ 到 $w_n$ 均会减小，也就是使得权重衰减，这样就会降低高阶项对于整个函数的影响，使得估计函数变得比较平滑。
我们还将λ除以 2 m, 这样这里的第一项和第二项都在 2 m 上按比例缩放，会更改容易选择λ的值。按照惯例我们不会因为参数 b 太大而惩罚它，在实践中，做与不做几乎没有什么区别。
因此，总结一下这个修改后的代价函数：
我们想要最小化[原始代价函数即均方误差项+第二项即正则化项]
λ : 可以控制两个不同目标之间的取舍。
此函数有两个目的，目的一：最小化预测值与真实值之间的误差，更好的拟合训练集。目的二：试图减小 $w_j$ ，使假设函数变得“简单”，防止过度拟合。
两者相互平衡，从而达到一种相互制约的关系，最终找到一个平衡点，从而更好地拟合训练集并且具有良好的泛化能力。
不同的λ值有什么影响？
使用线性回归的房价预测示例。
如果，λ等于 0，那么正则项等于零，即根本没有使用正则化，会过度拟合。
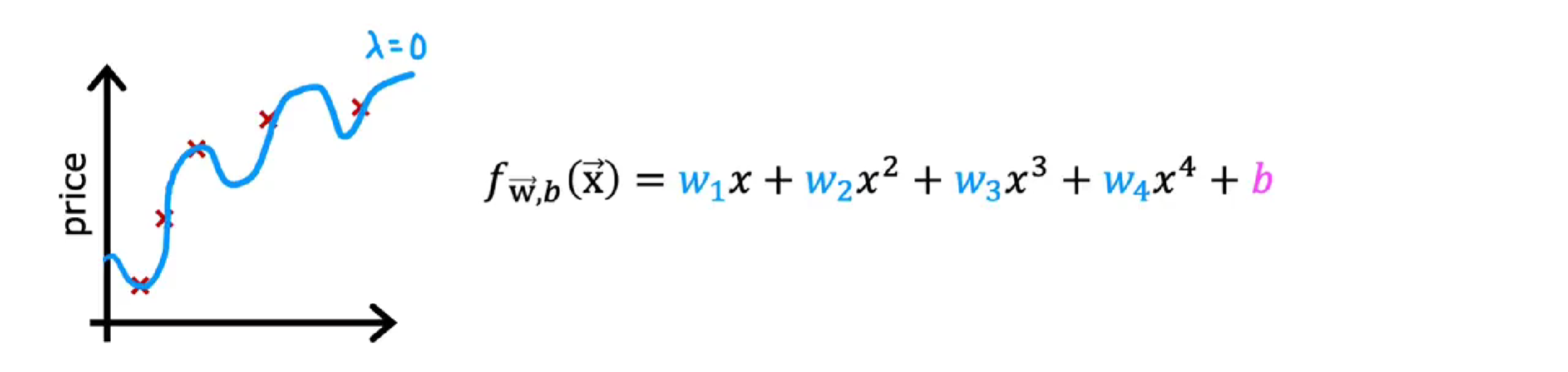
当λ非常非常大时，例如 $\lambda ={10}^{10}$,那么 $w_1\mathrm{到}{w}_4$ 几乎等于 0，只剩常数 b 项，此时会欠拟合。
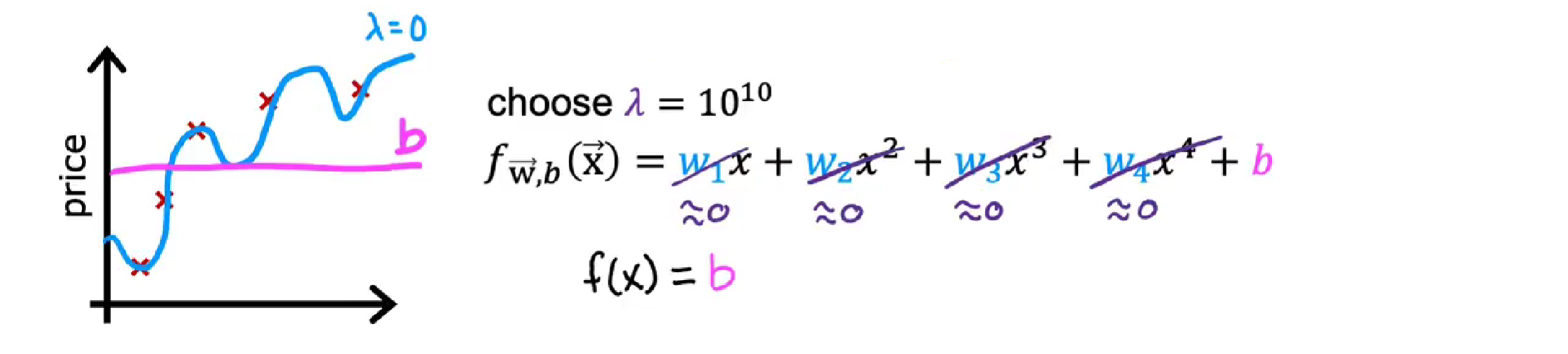
线性回归的正则化方法：

逻辑回归的正则化方法：

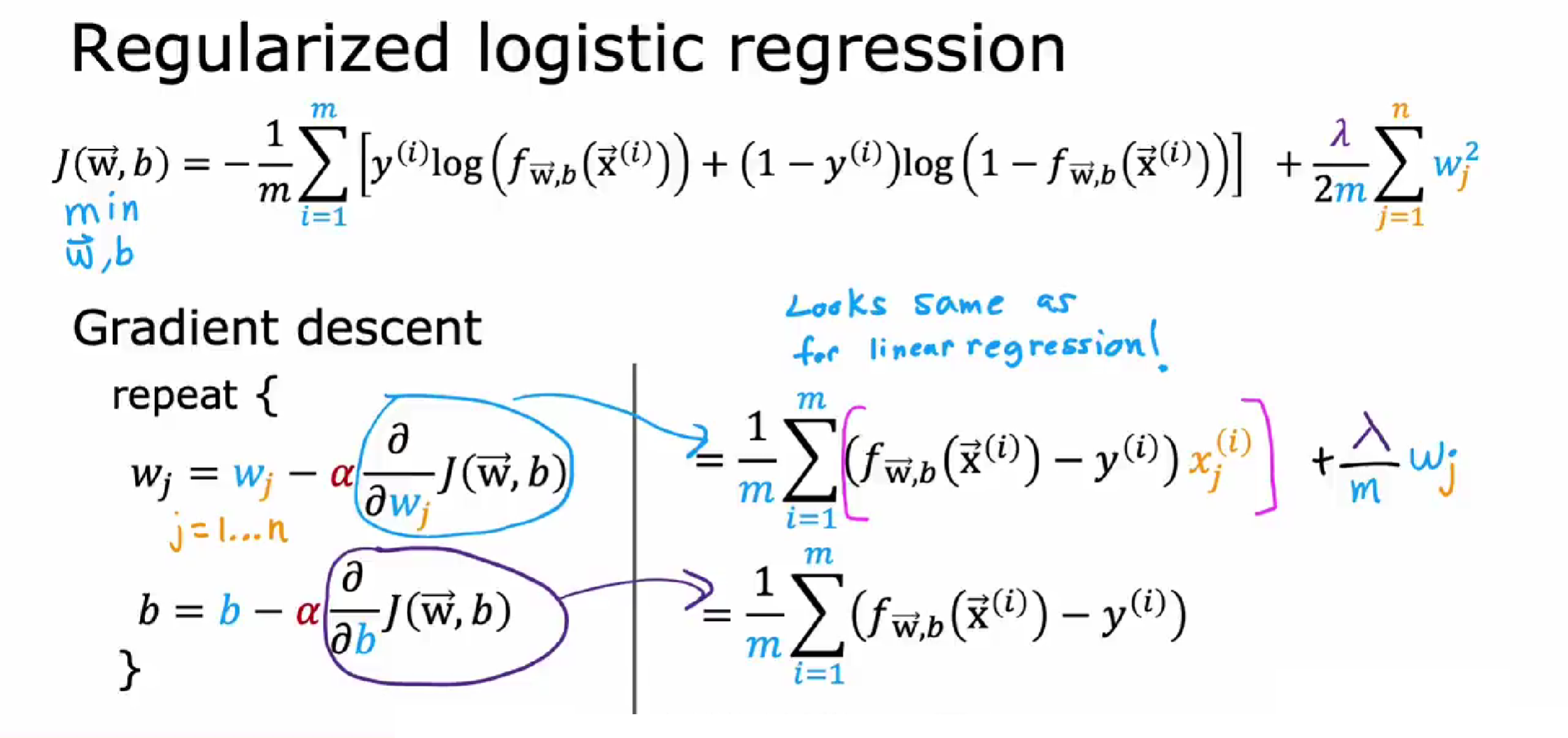
正则化如何影响方差和偏差


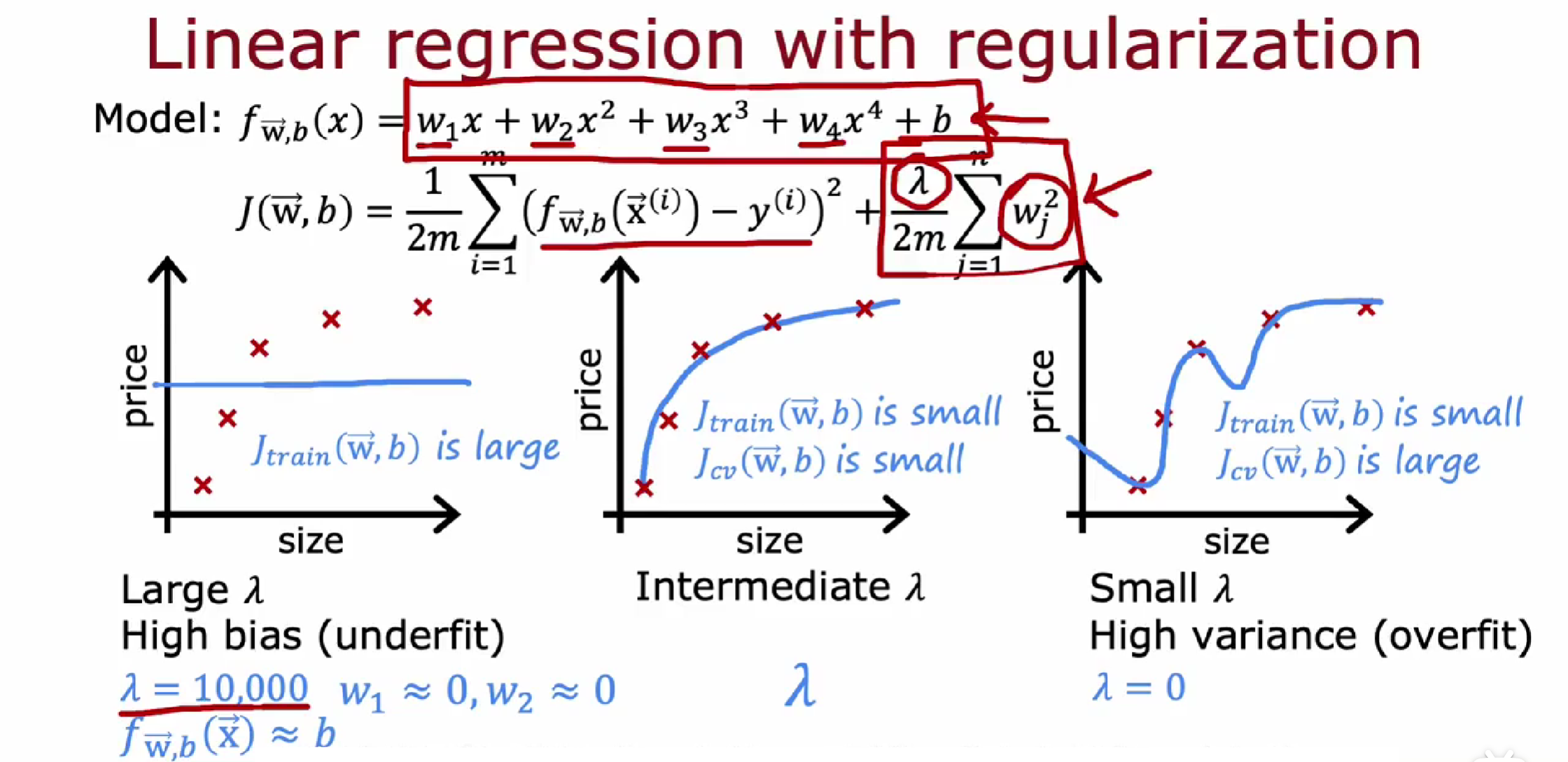
正则化中 $\lambda$ 评估

$\lambda$ 与代价函数值图：
$\lambda$ 小，过拟合，$J_{train}$ 低，$J_{cv}$ 高。
$\lambda$ 大，欠拟合，$J_{train}$ 高，$J_{cv}$ 高。